Hydrodynamics
Microorganisms swim in a low Reynolds number environment where viscous forces dominate. Hydrodynamic interactions in low Reynolds number environments influence the swimming behaviour of microorganisms and are important for synchronization and collective behaviour of flagella and cilia. We use simple hydrodynamic models to study complex behaviour in biological systems.
Microswimmers
We are interested in designs for autonomous swimmers in low Reynolds number conditions. Such swimmers can travel with net displacement only if the cycle of their deformations is non-reciprocal. This adds a significant complication when we want to design a machine with only a few degrees of freedom, like most human-engineered devices.
Non-reciprocal stroke cycle for the three-sphere swimmer (Ali Najafi, Zanjan Univ)
A simple model for a basic microswimmer is made of three spheres in a row connected by two rigid rods, which undergo a non-reciprocal stroke cycle. An experimental group in Cambridge, led by Pietro Cicuta, made a prototype of this model using optical tweezers and micron-sized colloidal particles. We have studied the feasibility of the model and various effects such as efficiency, response to external loads, and additional cargo.
The unicycle microswimmer
(Pietro Tierno, Univ of Barcelona)
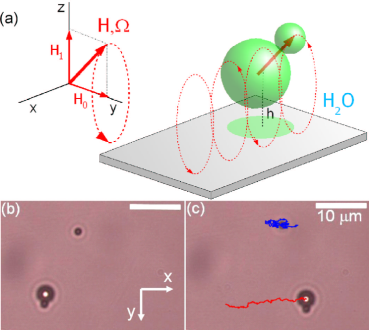
(Pietro Tierno, Univ of Barcelona)
Another idea to make a minimal microswimmer is a rotating colloidal dumbbell that interacts with a substrate. This microswimmer, which is reminiscent of a unicycle, takes advantage of stronger viscous friction at the bounding plate, as compared to fluid resistance in the bulk, to create an asymmetry in dissipation that rectifies rotation into a net translation of the suspended objects. Pietro Tierno and collaborators built this swimmer.
Microorganisms have evolved with non-reciprocal swimming strokes and we use simple hydrodynamic models to understand their swimming behaviour. For example, our collaborators in Gerard Wong’s lab observed two distinct motility types in Vibrio cholerae swimming near a surface. Our hydrodynamic model demonstrated that the nonlinearity of the interaction with the surface causes the two motility modes.
Group members involved: R. Golestanian
Synchronization
In low Reynolds number conditions, hydrodynamic interactions are long-ranged, which leads to emergent many-body behaviour. Examples of such cooperative dynamical effects include sperms beating in harmony, metachronal waves in cilia, formation of bound states between rotating microorganisms, and flocking behaviour observed in a variety of systems.
To capture the essence of the complex dynamics of active hydrodynamic components in high density, we consider a simple generic model of rotors positioned on a regular 2D array on a substrate and study their collective dynamics. We find that depending on how the rotors interact with the fluid, the system can be frustrated due to the long-ranged hydrodynamic interactions and this can lead to slow dynamics involving many defects. We find that the system could adopt a synchronized state or a dynamical state with turbulent spiral waves. We also take into account thermal fluctuations of the rotors and map out the phase diagram of the system as a function of temperature and the degree of frustration.
An important question is what are the necessary and sufficient conditions for synchronization? We have addressed this question for two rotors driven by phase dependent forcing. For rigid trajectories, phase dependent forcing is necessary for hydrodynamic synchronization.
Group members involved: R. Golestanian
Three-sphere model of Chlamydomonas: swimming, synchronization, run-and-tumble and phototaxis
Trajectory of the three-sphere model of Chlamydomonas with beat pattern coupling to light intensity. The light is in the direction of the orange arrow and is switched on during the red sections of trajectory, where we see negative phototaxis. The blue section in the trajectory has the light switched off and we see switching to run-and-tumble behaviour.
The simple three-sphere model of Chlamydomonas
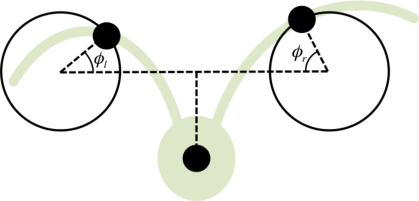
The flagella of Chlamydomonas beat in synchrony with a breaststroke-like motion. The rotation dynamics of the cell provide the mechanism for synchronization and the stability of the synchronized state has sensitive dependence on the beat pattern. When we add uncorrelated noise to a beat pattern parameter, we get emergent eukaryotic run-and-tumble behaviour.
When we couple the beat parameter to light intensity at the eyespot using a coupling that is consistent with experimental observations, the cell shows phototaxis and the steering is robust to noise. We use this simple model to explain a mechanism for phototactic steering.
This model is simple, yet it describes a variety of complex engineering requirements: low Reynolds swimming, synchronization, run-and-tumble and phototaxis.
Group members involved: R. Bennett, R. Golestanian
Stochastic Swimmers
Configuration space of a stochastic swimmer
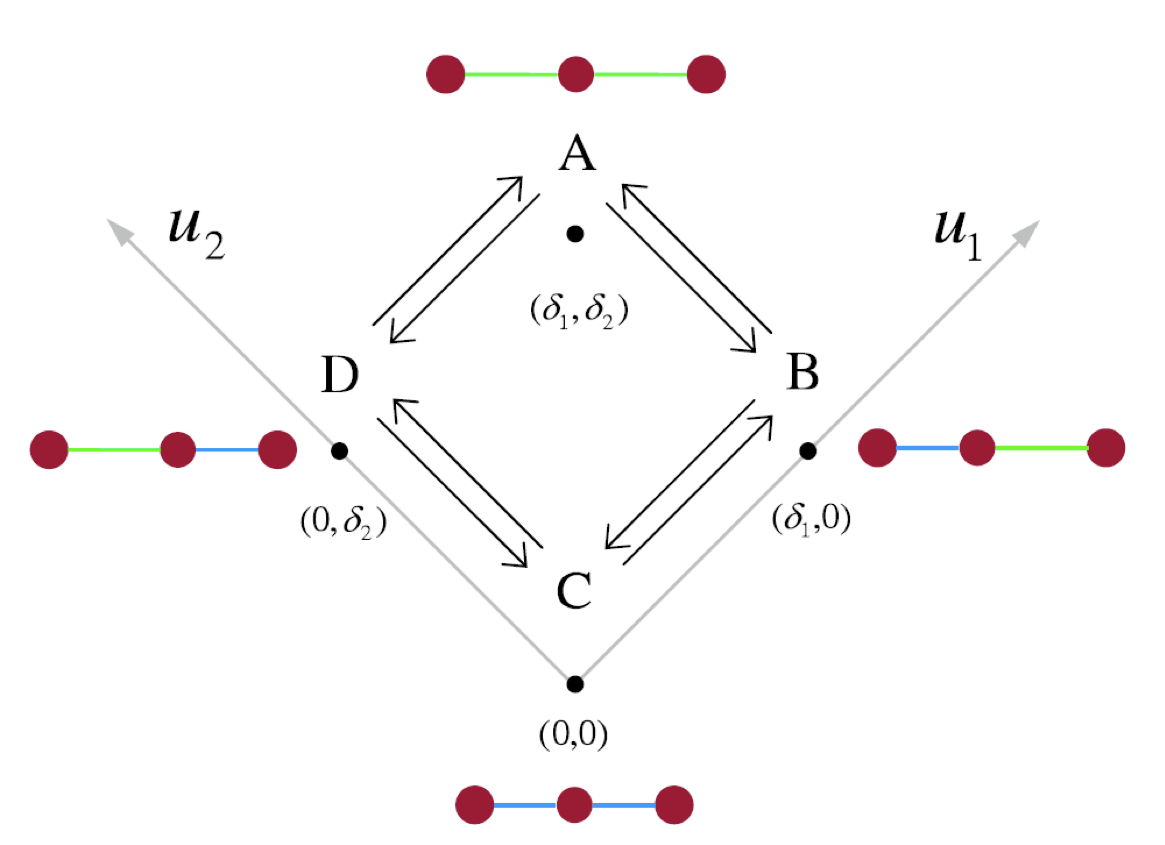
For molecular-scale swimmers, directed propulsion could not come from pre-specified deterministic periodic deformations because of thermal fluctuations, and there will be need to develop strategies to extract a net directed motion from a series of random transitions in the conformation space of the swimmer. The constructed stochastic motor model works when detailed-balance is broken and the motor is driven out of equilibrium. Interestingly, when such a system is put under the effect of an external load, the way stress is distributed across the swimmer's body will determine the efficiency of the different legs of the reaction cycle and hence the net swimming velocity. This shows that for the small swimmers that would be artificially made, the concept of generic force-velocity response breaks down, which might have intriguing implications for designing molecular swimmers.
We have also studied the concept of coherence between stochastic swimmers that are coupled via hydrodynamic interactions, and found that coherence could be introduced in the system through the correlations between the deformations, and that it can be used to create a stable bound state between two swimmers.
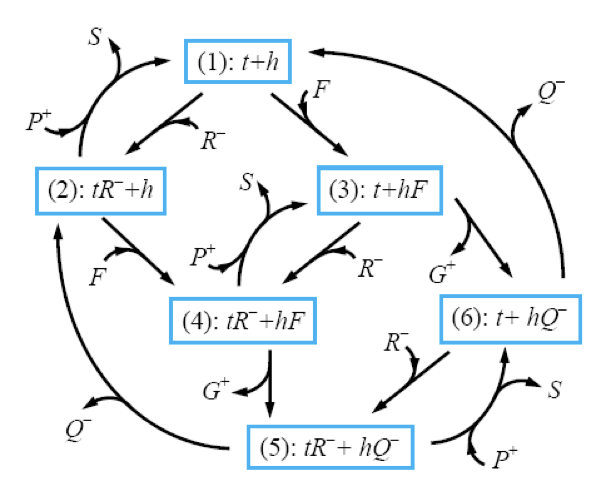
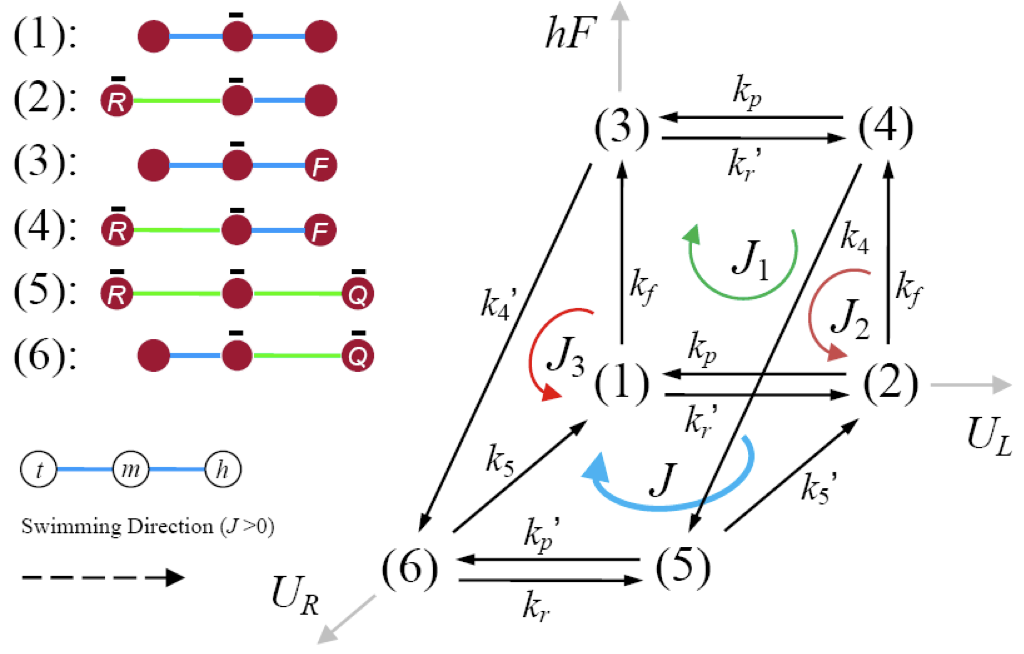
A minimal low Reynolds number swimmer model is also introduced that could take advantage of electrostatic interactions to induce conformational changes on the device. The swimmer has two enzymes on board that catalyze chemical reactions that involve ionic products. This allows the system to convert a biochemical cycle (above, left) to a mechano-chemical cycle (above, right), and develop a chemically powered molecular-scale actuation mechanisms. When the ions are still attached to the enzymes, electrostatic interaction between them and other charged elements of the swimmer can lead to conformational changes. The design proposes how one can take advantage of these stochastically temporarily charged components of the system and achieve net propulsion at low Reynolds number.
Group members involved: R. Golestanian