DPhil PROJECTS IN PLASMA PHYSICS
starting in October 2020 (for 2021, see here)
Application deadline: 24 January 2020
Oxford Plasma Theory Group welcomes applications for DPhil studies and research in plasma physics in the areas of magnetic confinement fusion (MCF) and plasma astrophysics (including "laboratory astrophysics")
Potential supervisors: Prof Michael Barnes (projects 1, 6), Prof Peter Norreys (project 3), Prof Felix Parra Diaz (project 2), Prof Alexander Schekochihin (projects 4, 5, 6, 7), Prof Gianluca Gregori (project 7)
Size of intake: this depends on various hard-to-predict circumstances, in particular funding arragements; we accepted 2 fully funded students in 2015, 4 in 2016, 3 in 2017, 3 in 2018, and 1 in 2019; we would like to take at least 2 this year.
*** MORE NEW PROJECTS MAY APPEAR ON THIS PAGE IN DUE COURSE. COME BACK AND CHECK! ***
- If you are interested in MCF (either theoretical or experimental) or generally in plasma physics, apply for a DPhil in Theoretical Physics. Note that Theoretical Physics has three separate DPhil competitions: in particle theory, condensed matter and plasma physics. If you are willing to be considered for more than one of these topics, please state so explicitly in your application form.
- If you are interested in ICF or
laboratory
astrophysics (projects with Prof Norreys and Prof Gregori), you may
also apply
for a DPhil in Atomic & Laser
Physics.
- If you are interested in plasma astrophysics, apply for a DPhil in Astrophysics. For the plasma astrophysics (and lab astro) projects, we recommend (but do not require) that you also apply for a DPhil in Theoretical Physics (indicating plasma physics as your preferred area) as this will help us identify your application more quickly and consider you for all available projects and funding options across plasma physics. We recmmend applying to both degrees if you are generally interested in plasma physics and are flexible between its different areas.
- Internal
Oxford scholarships: there are a number of scholarships in
physics
available at Oxford, including Clarendon
Scholarships, the James
Buckee
Scholarship at Merton College, the
Oxford-Berman Studentship at University College, the MPLS Division
EPSRC Excellence Scholatships and others. Note that in order to be
considered for a scholarship
funded by a particular College, you do not need to select that College
as your College of first choice, but you must indicate on your
application form that you are willing to move to another College to
gain an offer of funding (this simply requires that you leave blank the
box in the funding section of the University’s online application form
that must be ticked if you do not wish to be considered by another
college than your stated preferred one). There is one (known to us)
exception to this principle: if you
are studying at a Swiss university, apply to Lincoln College to
be eligible for a Berrow
Foundation Scholarship. If you are from India (or certain other developing
countries), make sure to indicate on your application that you wish to
be considered for a Felix
Scholarship.
- Choice
of College:
you may apply to any College that accepts graduate applicants in
Physics. Choice of college can prove important for your life as a
graduate student: different colleges offer different levels of support
in terms of research funds, accommodation, social integration etc. We
therefore recommend that you do not
leave the college choice blank,
but do some research on which college suits you best. We are happy to
give informal advice on the matter. Here is the list of Colleges where
the faculty members offering plasma projects this year are Fellows: Merton (A.
Schekochihin), LMH (G.
Gregori), Univ
(M. Barnes
and P.
Norreys), Worcester (F. Parra).
- If you are considering applying for an external scholarship and require our endorsement, in the first instance please contact the supervisor with whom you are most interested in working. Note the opportunities for Commonwealth Scholarships.
- You are welcome to address inquiries on science to any of the project supervisors listed below and on the logistical aspects of applying to Ms Michelle Bosher (but do please check first if your question is perhaps already answered here or here).
- All graduate students in plasma physics have access to graduate-level courses taught with the Oxford Master Course in Mathematical and Theoretical Physics (to which you can also apply as a stand-alone MSc degree) and the Oxford-Warwick-Imperial Centre for Postgraduate Training in Plasma Physics and High Energy Density Science.

Projects in Fusion Plasmas and Fundamental Plasma Physics

Our magnetic-confinement-fusion theory projects (1, 2 and 5) are offered jointly with researchers at the U.K.A.E.A. Culham Centre for Fusion Energy.
At the application stage, you are not required (although you may if you wish) to indicate which project you prefer --- we will consider all applicants purely on intellectual merit. If you are offered admission, we will strive to give you the opportunity to work on the project of your choice. Note that the project descriptions given below are not set in stone and we are willing to discuss modifications and adjustments to them that might better reflect your interests and inclinations.
1. Plasma
turbulence in 3D magnetic fields
Supervisor: Prof Michael Barnes
UKAEA co-supervisor: Dr Sarah Newton
Background Reading:
1. P. Helander, “Theory of plasma confinement in non-axisymmetric magnetic fields,” Rep. Prog. Phys. 77, 087001 (2014)
2. I. Abel et al., “Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows,” Rep. Prog. Phys. 76, 116201 (2013)
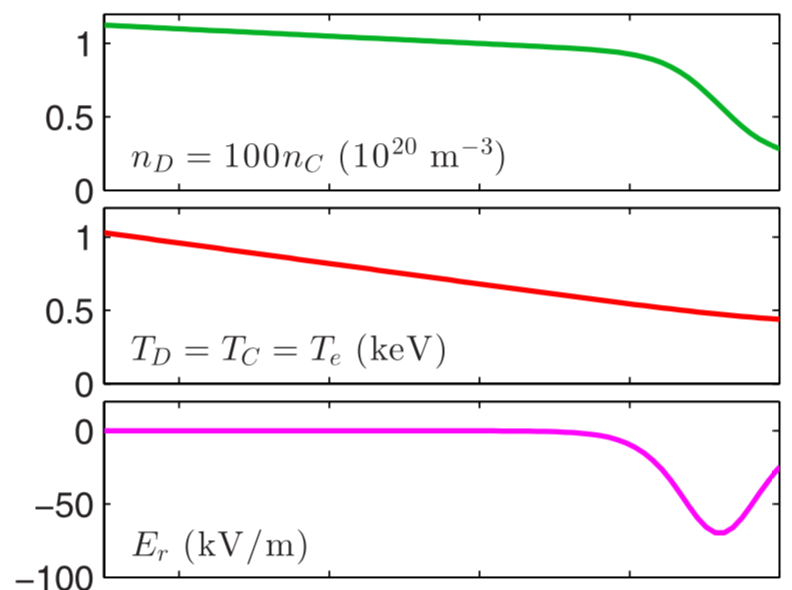
2. Theory of transition to reduced transport states in the edge of fusion devices
Supervisor: Prof Felix Parra Diaz
UKAEA co-supervisor: Dr Jon Hillesheim
Background Reading:
1. G. Kagan & P. J. Catto, "Arbitrary poloidal gyroradius effects in tokamak pedestals and transport barriers," PPCF 50, 085010 (2008)
2. M. Landreman et al., "Radially global delta f computation of neoclassical phenomena in a tokamak pedestal," PPCF 56, 045005 (2014)
3. D. Hatch et al., "A gyrokinetic perspective on the JET-ILW pedestal," PPCF 57, 036020 (2017)
4. I. Pusztai et al., "A current-driven electromagnetic mode in sheared and toroidal configurations," PPCF 56, 035011 (2014)
5. A. Geraldini, F. I. Parra, & F. Militello, "Gyrokinetic treatment of a grazing angle magnetic presheath," PPCF 59, 025015 (2017)
3. Maximising plasma turbulence in the hot spot of inertial fusion targets
Supervisor: Prof Peter Norreys
(for this project, you may also apply for a DPhil in Atomic and Laser Physics)
Background Reading:
1. N. Ratan et al., “Dense plasma heating by crossing relativistic electron beams,” Phys. Rev. E 95, 013211 (2017)
2. R. Olson et al., “First liquid layer inertial confinement fusion implosions at the National Ignition Facility,” Phys. Rev. Lett. 117, 245001 (2016)
4. Universal equilibria, phase-space structure of collisionless plasma systems, and turbulence in non-Maxwellian plasmas
Supervisor: Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Astrophysics)
Background Reading:
1. B. B. Kadomtsev & O. P. Pogutse, “Collisionless relaxation in systems with Coulomb interactions,” Phys. Rev. Lett. 25, 1155 (1970)
2. T. H. Dupree, “Theory of phase space density granulation in plasma,” Phys. Fluids 14, 334 (1972)
3. A. A. Schekochihin et al., “Phase mixing vs. nonlinear advection in drift-kinetic plasma turbulence,” J. Plasma Phys. 82, 905820212 (2016)
4. T. Adkins & A. A. Schekochihin, “A solvable model of Vlasov-kinetic plasma turbulence in Fourier-Hermite phase space,” J. Plasma Phys. 84, 905840107 (2018)
5. M. W. Kunz, A. A. Schekochihin, C. H. K. Chen, I. G. Abel and S. C. Cowley, “Inertial-range kinetic turbulence in pressure-anisotropic astrophysical plasmas,” J. Plasma Phys. 81, 325810501 (2015)
5. Coherent structures and fluctuating flows in near-critical ion-scale turbulence in tokamaks
Supervisor: Prof Alexander Schekochihin
UKAEA co-supervisor: Dr Anthony Field
Background Reading:
1. E. G. Highcock, M. Barnes, A. A. Schekochihin, F. I. Parra, C. M. Roach, and S. C. Cowley, "Transport bifurcation in a rotating tokamak plasma,'' Phys. Rev. Lett. 105, 215003 (2010)
2. Ferdinand van Wyk, E. G. Highcock, A. A. Schekochihin, C. M. Roach, A. R. Field, and W. Dorland, “Transition to subcritical turbulence in a tokamak plasma,” J. Plasma Phys. 82, 905820609 (2016)
3. Ferdinand van Wyk, E. G. Highcock, A. R. Field, C. M. Roach, F. I. Parra, W. Dorland, and A. A. Schekochihin, “Ion-scale turbulence in MAST: anomalous transport, subcritical transions, and comparison to BES measurements,” Plasma Phys. Control. Fusion 59, 114003 (2017)
4. M. F. J. Fox, F. van Wyk, A. R. Field, Y.-c. Ghim, F. I. Parra, A. A. Schekochihin, and the MAST Team, “Symmetry breaking in MAST plasma turbulence due to toroidal flow shear,” Plasma Phys. Control. Fusion 59, 034002 (2017)
Supervisor: Prof Michael Barnes
UKAEA co-supervisor: Dr Sarah Newton
Background Reading:
1. P. Helander, “Theory of plasma confinement in non-axisymmetric magnetic fields,” Rep. Prog. Phys. 77, 087001 (2014)
2. I. Abel et al., “Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows,” Rep. Prog. Phys. 76, 116201 (2013)
2. Theory of transition to reduced transport states in the edge of fusion devices
Supervisor: Prof Felix Parra Diaz
UKAEA co-supervisor: Dr Jon Hillesheim
Background Reading:
1. G. Kagan & P. J. Catto, "Arbitrary poloidal gyroradius effects in tokamak pedestals and transport barriers," PPCF 50, 085010 (2008)
2. M. Landreman et al., "Radially global delta f computation of neoclassical phenomena in a tokamak pedestal," PPCF 56, 045005 (2014)
3. D. Hatch et al., "A gyrokinetic perspective on the JET-ILW pedestal," PPCF 57, 036020 (2017)
4. I. Pusztai et al., "A current-driven electromagnetic mode in sheared and toroidal configurations," PPCF 56, 035011 (2014)
5. A. Geraldini, F. I. Parra, & F. Militello, "Gyrokinetic treatment of a grazing angle magnetic presheath," PPCF 59, 025015 (2017)
3. Maximising plasma turbulence in the hot spot of inertial fusion targets
Supervisor: Prof Peter Norreys
(for this project, you may also apply for a DPhil in Atomic and Laser Physics)
Background Reading:
1. N. Ratan et al., “Dense plasma heating by crossing relativistic electron beams,” Phys. Rev. E 95, 013211 (2017)
2. R. Olson et al., “First liquid layer inertial confinement fusion implosions at the National Ignition Facility,” Phys. Rev. Lett. 117, 245001 (2016)
4. Universal equilibria, phase-space structure of collisionless plasma systems, and turbulence in non-Maxwellian plasmas
Supervisor: Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Astrophysics)
Background Reading:
1. B. B. Kadomtsev & O. P. Pogutse, “Collisionless relaxation in systems with Coulomb interactions,” Phys. Rev. Lett. 25, 1155 (1970)
2. T. H. Dupree, “Theory of phase space density granulation in plasma,” Phys. Fluids 14, 334 (1972)
3. A. A. Schekochihin et al., “Phase mixing vs. nonlinear advection in drift-kinetic plasma turbulence,” J. Plasma Phys. 82, 905820212 (2016)
4. T. Adkins & A. A. Schekochihin, “A solvable model of Vlasov-kinetic plasma turbulence in Fourier-Hermite phase space,” J. Plasma Phys. 84, 905840107 (2018)
5. M. W. Kunz, A. A. Schekochihin, C. H. K. Chen, I. G. Abel and S. C. Cowley, “Inertial-range kinetic turbulence in pressure-anisotropic astrophysical plasmas,” J. Plasma Phys. 81, 325810501 (2015)
5. Coherent structures and fluctuating flows in near-critical ion-scale turbulence in tokamaks
Supervisor: Prof Alexander Schekochihin
UKAEA co-supervisor: Dr Anthony Field
Background Reading:
1. E. G. Highcock, M. Barnes, A. A. Schekochihin, F. I. Parra, C. M. Roach, and S. C. Cowley, "Transport bifurcation in a rotating tokamak plasma,'' Phys. Rev. Lett. 105, 215003 (2010)
2. Ferdinand van Wyk, E. G. Highcock, A. A. Schekochihin, C. M. Roach, A. R. Field, and W. Dorland, “Transition to subcritical turbulence in a tokamak plasma,” J. Plasma Phys. 82, 905820609 (2016)
3. Ferdinand van Wyk, E. G. Highcock, A. R. Field, C. M. Roach, F. I. Parra, W. Dorland, and A. A. Schekochihin, “Ion-scale turbulence in MAST: anomalous transport, subcritical transions, and comparison to BES measurements,” Plasma Phys. Control. Fusion 59, 114003 (2017)
4. M. F. J. Fox, F. van Wyk, A. R. Field, Y.-c. Ghim, F. I. Parra, A. A. Schekochihin, and the MAST Team, “Symmetry breaking in MAST plasma turbulence due to toroidal flow shear,” Plasma Phys. Control. Fusion 59, 034002 (2017)

Projects in Plasma Astrophysics

Candidates interested in any of these projects or generally in plasma astrophysics, astrophysical turbulence and/or dynamo theory are welcome to get in touch with prospective supervisors for further information. A more bespoke project can be designed to align with the inclinations and interests of the student (for example how much emphasis is placed on analytical vs. numerical methods or kinetic theory vs. fluid dynamics, etc., is negotiable).
6.
Free-energy flows in
turbulent astrophysical plasmas
Supervisors: Prof Michael Barnes and Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Astrophysics)
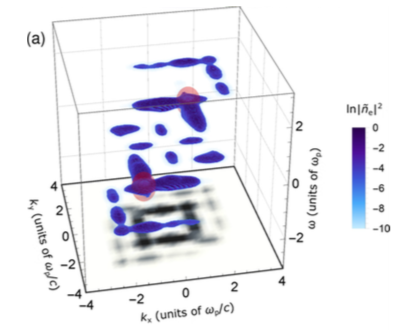
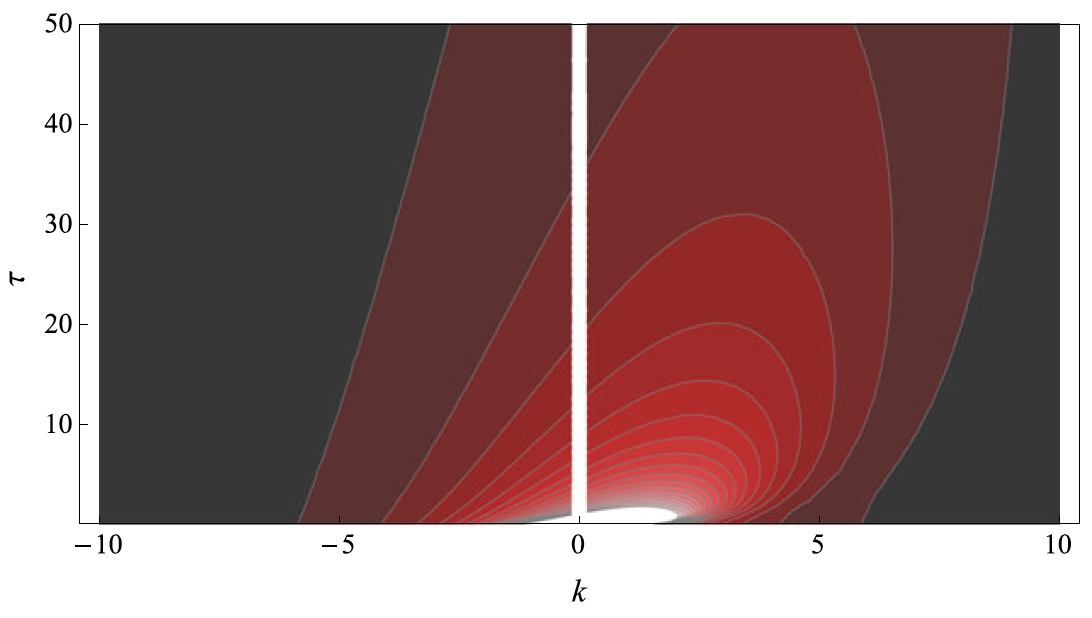
In magnetised astrophysical plasmas, there is a turbulent cascade of electromagnetic fluctuations carrying free energy from large to small scales. The energy is typically extracted from large-scale sources (e.g., in the solar wind, the violent activity in the Sun’s corona; in accretion discs, the Keplerian shear flow; in galaxy clusters, outbursts from active galactic nuclei) and deposited into heat – the internal energy of ions and electrons. In order for this dissipation of energy to happen, the energy must reach small scales – in weakly collisional plasmas, these are small scales in the 6D kinetic phase space, i.e., what emerges are large spatial gradients of electric and magnetic fields and large gradients of the particle distribution functions with respect to velocities. This prompts two very intriguing questions: (1) how does the energy flow through the 6D phase space and what therefore is the structure of the fluctuations in this space: their spectra, phase-space correlation functions etc. (these fluctuations are best observed in the solar wind, but these days we can also measure density and magnetic fluctuations in galaxy clusters, via X-ray and radio observations); (2) when turbulent fluctuations are dissipated into particle heat, how is their energy partitioned between various species of particles that populate the plasma: electrons, bulk ions, minority ions, fast non-thermal particles (e.g., cosmic rays). The latter question is particularly important for extragalactic plasmas because all we can observe is radiation from the particles and knowing where the internal energy of each species came from is key to constructing and verifying theories both of turbulence and of macroscale dynamics and thermodynamics. This project has an analytical and a numerical dimension (which of these will dominate depends on the student’s inclinations). Analytically, we will work out a theory of phase space cascade at spatial scales between the ion and electron Larmor scales (we have done some preliminary work, so we know how to start off on this calculation, but obviously at some point we’ll be wading into unchartered waters). Numerically, we will simulate this cascade using “gyrokinetic” equations – an approach in which we average over the Larmor motion and calculate the distribution function of “Larmor rings of charge” rather than particles (this reduces the dimension of phase space to 5D, making theory more tractable and numerics more affordable).
Background Reading:
1. A. A. Schekochihin et al., “Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas,” Astrophys. J. Suppl. 182, 310 (2009)
2. A. A. Schekochihin et al., “Phase mixing vs. nonlinear advection in drift-kinetic plasma turbulence,” J. Plasma Phys. 82, 905820212 (2016)
3. Y. Kawazura, M. Barnes, and A. A. Schekochihin, “Thermal disequilibration of ions and electrons by collisionless plasma turbulence,” PNAS 116, 771 (2019)
4. R. Meyrand, A. Kanekar, W. Dorland, and A. A. Schekochihin, “Fluidization of collisionless plasma turbulence,” PNAS 116, 1185 (2019)
5. A. A. Schekochihin, Y. Kawazura, and M. A. Barnes, “Constraints on ion vs. electron heating by plasma turbulence at low beta,” J. Plasma Phys. 85, 905850303 (2019)
Supervisors: Prof Michael Barnes and Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Astrophysics)
In magnetised astrophysical plasmas, there is a turbulent cascade of electromagnetic fluctuations carrying free energy from large to small scales. The energy is typically extracted from large-scale sources (e.g., in the solar wind, the violent activity in the Sun’s corona; in accretion discs, the Keplerian shear flow; in galaxy clusters, outbursts from active galactic nuclei) and deposited into heat – the internal energy of ions and electrons. In order for this dissipation of energy to happen, the energy must reach small scales – in weakly collisional plasmas, these are small scales in the 6D kinetic phase space, i.e., what emerges are large spatial gradients of electric and magnetic fields and large gradients of the particle distribution functions with respect to velocities. This prompts two very intriguing questions: (1) how does the energy flow through the 6D phase space and what therefore is the structure of the fluctuations in this space: their spectra, phase-space correlation functions etc. (these fluctuations are best observed in the solar wind, but these days we can also measure density and magnetic fluctuations in galaxy clusters, via X-ray and radio observations); (2) when turbulent fluctuations are dissipated into particle heat, how is their energy partitioned between various species of particles that populate the plasma: electrons, bulk ions, minority ions, fast non-thermal particles (e.g., cosmic rays). The latter question is particularly important for extragalactic plasmas because all we can observe is radiation from the particles and knowing where the internal energy of each species came from is key to constructing and verifying theories both of turbulence and of macroscale dynamics and thermodynamics. This project has an analytical and a numerical dimension (which of these will dominate depends on the student’s inclinations). Analytically, we will work out a theory of phase space cascade at spatial scales between the ion and electron Larmor scales (we have done some preliminary work, so we know how to start off on this calculation, but obviously at some point we’ll be wading into unchartered waters). Numerically, we will simulate this cascade using “gyrokinetic” equations – an approach in which we average over the Larmor motion and calculate the distribution function of “Larmor rings of charge” rather than particles (this reduces the dimension of phase space to 5D, making theory more tractable and numerics more affordable).
Background Reading:
1. A. A. Schekochihin et al., “Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas,” Astrophys. J. Suppl. 182, 310 (2009)
2. A. A. Schekochihin et al., “Phase mixing vs. nonlinear advection in drift-kinetic plasma turbulence,” J. Plasma Phys. 82, 905820212 (2016)
3. Y. Kawazura, M. Barnes, and A. A. Schekochihin, “Thermal disequilibration of ions and electrons by collisionless plasma turbulence,” PNAS 116, 771 (2019)
4. R. Meyrand, A. Kanekar, W. Dorland, and A. A. Schekochihin, “Fluidization of collisionless plasma turbulence,” PNAS 116, 1185 (2019)
5. A. A. Schekochihin, Y. Kawazura, and M. A. Barnes, “Constraints on ion vs. electron heating by plasma turbulence at low beta,” J. Plasma Phys. 85, 905850303 (2019)
7. Magnetised
plasma turbulence: from laser lab to galaxy clusters
Supervisors: Prof Gianluca Gregori and Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Atomic and Laser Physics or a DPhil in Astrophysics)
Supervisors: Prof Gianluca Gregori and Prof Alexander Schekochihin
(for this project, you may also apply for a DPhil in Atomic and Laser Physics or a DPhil in Astrophysics)
There are a number of
possibilities within this project to design, take part in and theorise
about laboratory experiments employing laser-produced plasmas to model
astrophysical phenomena and basic, fundamental physical processes in
turbulent plasmas. Recent examples of our work in this field include
turbulent generation of magnetic fields ("dynamo") [1,2], supersonic
turbulence mimicking star-forming molecular clouds, diffusion and
acceleration of particles by turbulence [3,4]. Our group has access to
several laser facilities (including the National Ignition Facility, the
largest laser system in the world). Students will also have access to a
laser laboratory on campus, where initial experiments can be fielded.
Background Reading:
1. G. Gregori et al., “The generation and amplification of intergalactic magnetic fields in analogue laboratory experiments with high power lasers,” Phys. Reports 601, 1 (2015)
2. P. Tzeferacos et al., “Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma,” Nature Comm. 9, 591 (2018)
3. A. F. A. Bott et al., “Proton imaging of stochastic magnetic fields,” J. Plasma Phys. 83, 905830614 (2017)
4. L. E. Chen et al., “Stochastic transport of high-energy particles through a turbulent plasma,” arXiv:1808.04430
1. G. Gregori et al., “The generation and amplification of intergalactic magnetic fields in analogue laboratory experiments with high power lasers,” Phys. Reports 601, 1 (2015)
2. P. Tzeferacos et al., “Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma,” Nature Comm. 9, 591 (2018)
3. A. F. A. Bott et al., “Proton imaging of stochastic magnetic fields,” J. Plasma Phys. 83, 905830614 (2017)
4. L. E. Chen et al., “Stochastic transport of high-energy particles through a turbulent plasma,” arXiv:1808.04430