Oxford Theoretical Physics
Condensed Matter Theory
Steve Simon
Research:
Links:
When we first learn classical mechanics we might get the feeling that knowing the constituent equations (Newton's equations in this case) is sufficient to fully understand all the physics of the motion of bodies. However, we soon discover that when many bodies are considered at the same time, and are allowed to interact with one another, these equations become very complicated very quickly. Naively one may consider this only a computational problem, but interesting physics - indeed, some of the most interesting physics of classical mechanics - is buried in the complexity of these equations. For example, taking a macroscopic approach to the problem, and identifying the right degrees of freedom of a many molecule system, the equations of motion of interacting molecules forming a fluid can be described by the Navier-Stokes equations for fluid dynamics from which complex new behaviors arise such as turbulence. This is perhaps the simplest example of an emergent phenomenon.
When quantum mechanics is included into the mix, the situation becomes even more complicated, and correspondingly, more interesting. Here, the underlying equation is the Schroedinger equation - but the complexity of solving this equation now increases exponentially with the number of interacting particles being considered. Again one may be tempted to think of this only as a computational issue, but at some point one must ask if a problem is only computational if the largest computer that could ever be built would not be able to solve it (excluding the possibility of a quantum computer).
One approach for tackling such a problem is to identify a small parameter in the problem and first treat this parameter as zero - simplifying the problem and perhaps making it tractable. For example, one might take a weakly interacting system and model it as a solvable noninteracting system, then treat the interaction as a small perturbation. While this approach is one of the most frequently used tools of a physicist's toolbox, it is only reliable for systems sufficiently "near" to the non-interacting, or solvable, situation. Systems where the interaction is strong are often resistant to this method of attack, and indeed such nonperturbative problems are often found in condensed matter systems.
Despite the difficulty of this problem, remarkable progress has been made in understanding strongly interacting quantum systems, and this is the main purview of the quantum condensed matter physicist (Footnote: I like to call myself a quantum condensed matter physicist - although sometimes I like calling myself an "hbar condensed matter physicist," referring to Planck's constant as the unit of quantum action). Some of the major successes in the history of quantum condensed matter physics include the Landau theory of Fermi liquids, the BCS theory of superconductivity, the theory of superfluidity, and the Laughlin theory of fractional quantum Hall effect. In each of these cases, a strongly interacting system can be well understood in terms of weakly interacting so-called quasiparticle excitations. In some of these cases, the quasiparticles bear almost no resemblance to the underlying degrees of freedom of the system - they have emerged as a complex collective effect.
Perhaps the most striking example of emergent phenomena is in fractional quantum Hall systems - two dimensional systems of electrons at low temperature and in high magenetic fields. In this case, the underlying degrees of freedom are the electron, but the emergent quasiparticles have charge which is only a fraction of that of the electron. The fractionalization of the elementary electron is perhaps one of the most shocking discoveries of modern physics, and is purely a collective emergent effect. Even more interesting is that the quantum properties of these fractionalized quasiparticles are unlike any ever found elsewhere in nature!
Topological Phases of Matter:
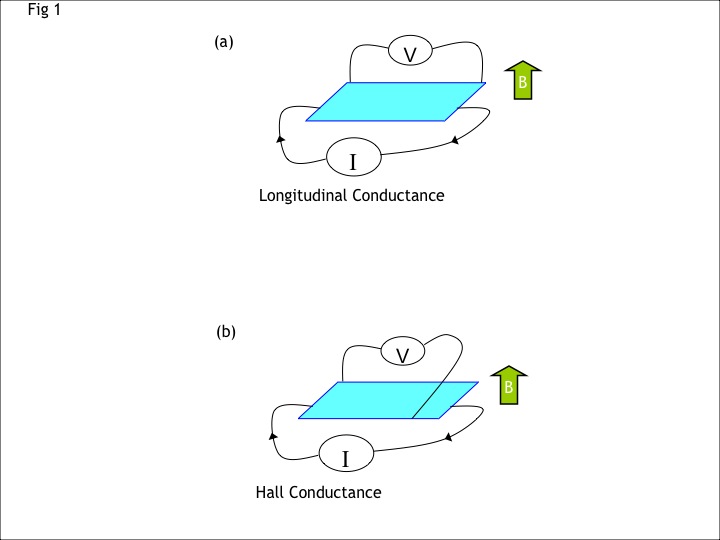
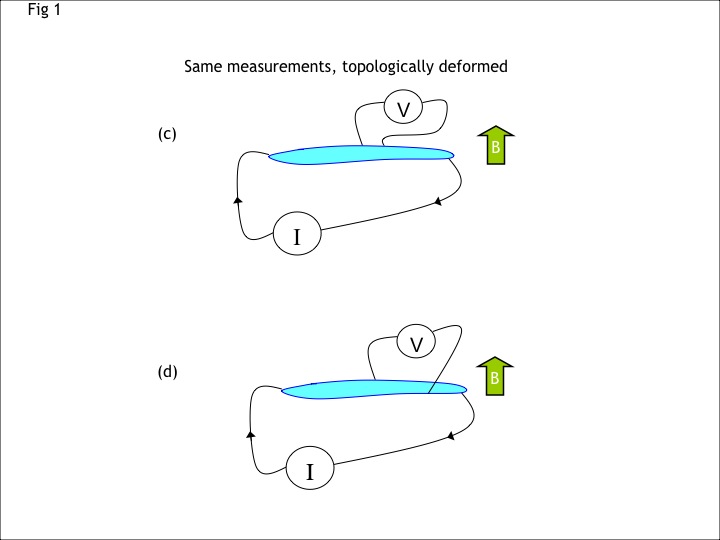
FIG 1: Two measurements of conductance are shown, Longitudinal Conductance (a) and Hall conductance (b). Panels (c) and (d) are also longitudinal and Hall conductance but the sample and the positions of the leads have been topologically (i.e., smoothly) deformed. For typical metals, the topological deformation will change the measured conductance. However, for topological phases of matter, such as fractional quantum Hall states, the measured conductance is unchanged by topological deformation.
Topology is the branch of mathematics that studies those properties that remain unchanged under smooth continuous deformations. Many physically measurable properties of real materials are not topologically invariant - that is, they change if the system is smoothly deformed. For example, the electrical conductance of a piece of metal depends on the shape of the piece and precisely where you put the contacts. If you smoothly deform the position of the contacts or the shape of the sample, the measured result will change. Remarkably, however, there are certain states of matter, known as topological phases, for which measurement of conductance gives a topologically invariant result. Perhaps the best studied topological phases of matter are the various quantum Hall states, the discovery of which has resulted in several Nobel prizes already. In such two-dimensional systems, as shown in Fig. 1, the longitudinal conductance is always zero, and the Hall conductance is always given by νe2/ħ where ν is a rational number, known as the filling fraction, that characterizes the particular quantum Hall phase of matter being measured (e is the electron charge and ħ is Planck's constant). These results are independent of the precise shape of the sample, position of the contact, disorder in the sample, or other small perturbations. Indeed, the effect is so robust that it is used as a metrological standard for resistance, being able to give measurements that are consistently reproducible to better than 1 part in 1010.
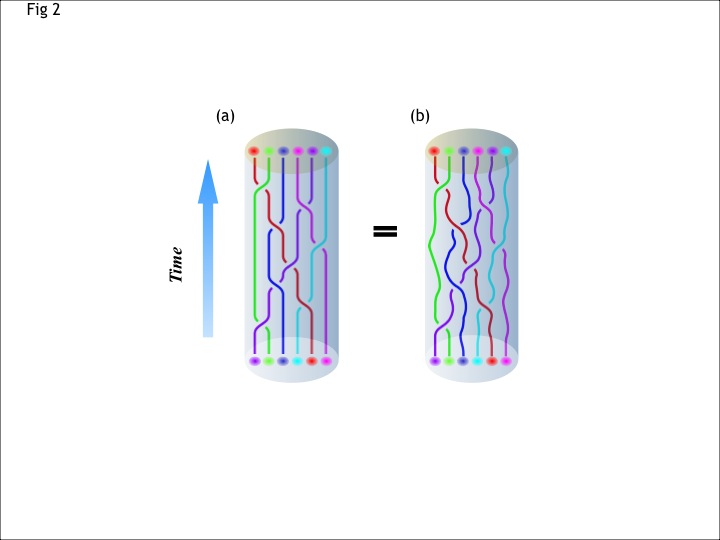
FIG 2: [Artwork provided by Layla Hormozi]. (a) World lines for (quasi)-particles in 2+1 dimensions. Here the system in question is a two dimensional disk with six colored particles. Time is shown in the vertical direction so that these world-lines describe a particular space-time path. The particles are meant to be identical objects but are colored so one can more easily follow them (b) The second space-time path is geometrically different from, but topologically identical to, the first.
While topological invariance of conductance is perhaps the most experimentally obvious property of a topological phase of matter, the invariance is not only an invariance under deformation of space, but also under deformation of space-time. Let us consider a set of world-lines describing the a space-time path connecting an initial configuration of (quasi)-particles to a final configuration of (quasi)-particles, as shown in Fig 2a. In the Feynman path-integral formulation of quantum mechanics, each possible path is assigned a quantum mechanical complex amplitude. In a topological phase of matter, the amplitude depends only on the space-time topology of the path, and not on the detailed geometry. Thus for topological phases of matter the amplitude for the process shown in Fig 2b is the same as that for Fig 2a. The relation between the topology of a space time path and an amplitude defines a "topological quantum field theory."
Topological phases of matter, and correspondingly topological quantum field theories, come in two varieties. The simpler variety is known as Abelian and the more complicated is known as non-Abelian. The Abelian variety is more similar to most phases of matter that we are familiar with: In this case, given that the (quasi)-particles have some particular positions in space there is a unique ground state wavefunction, up to a prefactor which is simply a complex unit magnitude phase. The process of dragging the particles around each other and returning them to their original positions (as in Fig 2a) simply introduces a phase that depends on the number of clockwise versus counterclockwise wrappings. If the particles are bosons the phase is always +1 and if the particles are fermions the phase is +1 or -1 depending on whether the total number of particle exchanges is even or odd. However, more generally in Abelian 2+1 dimensions topological phases of matter, any complex phase can be associated with wrapping particles around each other and the corresponding quantum (quasi)-particles are called anyons. Our current state of understanding, based on a great deal of experimental and theoretical work, is that anyons really do exist (and hence Abelian topological phases of matter really do exist) in most fractional quantum Hall systems.
The non-Abelian topological phases of matters, and corresponding topological quantum field theories, have an additional crucial property that once the position of the (quasi)-particles are fixed, there remains a degeneracy of the ground state of the system. As such, the ground state wavefunction is specified as some vector in this degenerate space. Dragging particles around each other (as shown in Fig 2) then acts as a unitary matrix applied to the vector in this degenerate space. Since matrices generally do not commute, this type of behavior is known as non-Abelian (which is a fancy work for non-commutative), and (quasi)-particles that behave this way are known as non-Abelian anyons. Although such a complicated structure seems rather exotic, there is growing evidence that a few fractional quantum Hall states of matter, in particular the nu=5/2 state, really do have these properties.
The idea of topological phases of matter grew from the high-energy physics theory community where topological quantum field theories were studied, starting in the 1980s, partially for their mathematical interest (indeed a Fields medal of mathematics was awarded to Witten for work in this field) but also as toy models of more complicated quantum field theories that might describe our universe. The idea that such topological quantum field theories could also describe certain phases of matter (topological phases of matter) that can be realized in the laboratory has taken hold only slowly over the last twenty years as evidence has emerged that they may indeed exist in nature.
Topological Quantum Computation:
In non-Abelian topological phases of matter, the existence of a degenerate ground state subspace suggests the possibility of using this space for storing and processing quantum information. By dragging particles around each other to form space-time braids (as in Fig 2) one can manipulate the wavefunction vector in the ground state subspace in a controlled way. Each particular braid corresponds to a particular matrix operation, or quantum computation, on this ground state space. For example, shown in Fig 3 is a space-time braid that performs an extremely simple quantum operation, known as a controlled NOT. Similarly even the most complicated quantum algorithm, such as Shor's famous factoring algorithm, can be reduced to a particular braid.
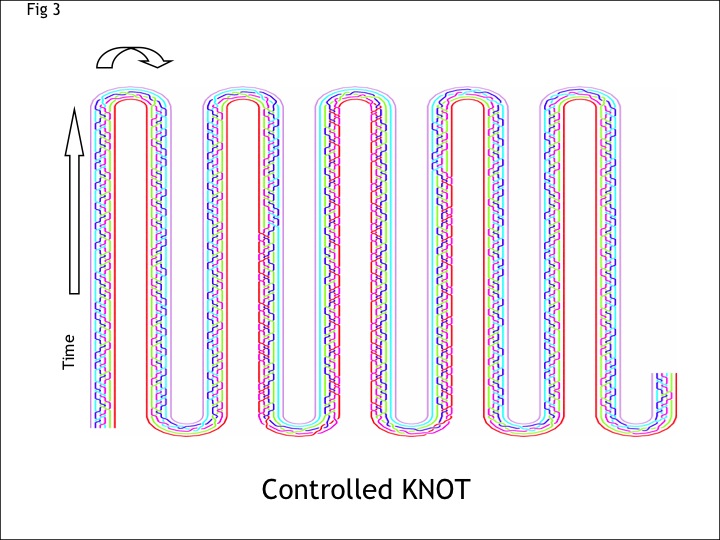
FIG 3: This picture is a blueprint of instructions for moving particles around each other in order to perform a particularly simple quantum computation known as a controlled NOT. In the approach of topological quantum computing, all computations are reduced to knots in this way (The title "Controlled KNOT" is a pun).
The idea of topological quantum computing, credited to Alexei Kitaev and Michael Freedman (another Fields medallist), while probably difficult to realize in practice, nonetheless has some strong theoretical appeal. Although there are many proposed approaches to quantum information processing and quantum computation, essentially all of them suffer from the same problem, known as the decoherence problem, which is essentially just their exquisite sensitivity of quantum systems to even miniscule noise, and coupling with the environment. The huge advantage of using topological phases for storing quantum information is that the degenerate ground state subspace is naturally isolated from almost all possible noise sources and error processes. As shown in Fig 2, if the system is hit by thermal noise, the space-time paths may become wiggly rather than smooth, but this does not at all change the operation that is performed. The most serious error processes that occur in these systems is when a stray particle gets thermally excited and forms an "unintentional" space-time braid with several other stationary particles (although such processes can presumably go away exponentially at low temperature). Another advantage of this topological scheme is that the operations that can be performed on the ground state space are naturally quantized since topologically a particle either encircles another particle or it does not - there is no way to miss by a small amount. This quantization of the operation renders the system immune to small errors caused by making slight control errors in manipulating the particles.
Topological quantum computation can be thought of as an "ideal" way to perform quantum computation, that is naturally protected from decoherence and error. Unfortunately, the theoretical appeal of this method is roughly countered by the practical difficulties. Experimental efforts are currently underway attempting to show even a proof-of-principle that quantum Hall states do indeed have these non-Abelian properties. After several years of work by several of the top experimental groups worldwide, results have remained inconclusive as the actual systems are apparently far more complex than theorists had originally assumed.
