Active systems are collections of particles that continuously take energy from their surrounding and use it to do work. Examples include bacterial colonies and living cells. Hydrodynamic instabilities are inherent to active fluids, and active suspensions spontaneously generate complex flow patterns at length scales much larger than the microscopic constituents. These are characterised by strong variations in vorticity and topological defects that are self-propelling. Such turbulent-like patterns have been observed in experiments on mixtures of actin or microtubules and motor proteins designed to isolate the important ingredients leading to cellular motility and in dense suspensions of swimming E-coli.

We have recently shown that layers of cells show many of the features of dense active matter. In particular it is possible to identify motile topological defects. These are correlated with cells which die and are ejected from the layer, a process vital in promoting healthy tissue and avoiding the formation of tumours.

We are also interested in active material in confined spaces where the interplay of the active and the confining length scales, together with the possible creation of motile topological defects, can lead to surprisingly complex behaviour. For example in narrow channels a one-dimensional line of flow vortices forms a racetrack for defects which move right or left on sinusoidal trajectories.

More details can be found in our review: Active nematics, Nature Communications 9 3246 (2018) and in our recent papers

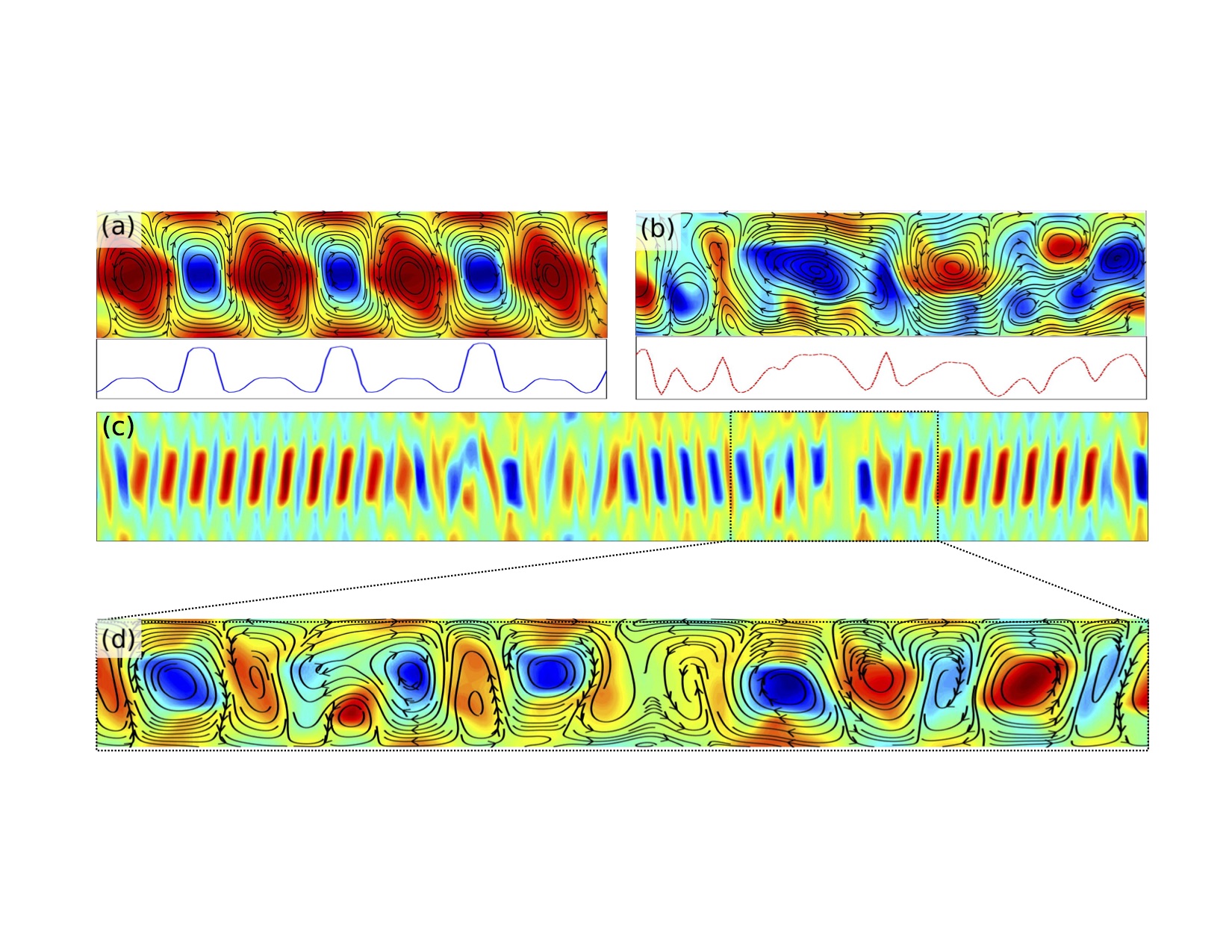
Emergence of active puffs from a vortex-lattice controls the transition to turbulence in living fluids. (a) A highly ordered flow vortex-lattice is formed at lower activities when an active fluid is confined and (b) active turbulence is fully established at higher activities. Lower panels in (a), (b) show the height-averaged enstrophy signal along the channel. (c) Coexistence of the vortex-lattice and meso-scale turbulence close to the transition point. The zoomed-in panel in (d) illustrates the formation of active puffs from the vortex-lattice. Colormaps show vorticity contours with blue and red colors corresponding to clockwise and anti-clockwise vortices, respectively. The average radius of vortices is 0:32h, where h denotes the channel height.

Growth, motion and morphogenesis are features common to all biological systems. Chemical energy allows biological cells to function out of thermodynamic equilibrium and to alter their number, size, shape and location. For example the marine polyp Hydra can re-form its body and grow tentacles starting from a small, excised piece of tissue. The zygote that results when a mammalian egg and sperm cell fuse, divides to form a ball of cells, the blastocyst. Collective cell migrations and remodelling then drive the tissue folding that determines how cells are positioned before they differentiate to grow into the stunning diversity of different living creatures. The development of organoids and tumours is controlled by the confining properties of the viscous, extracellular matrix that surrounds tissues, and escape into the third dimension determines the growth of biofilms. The relevance of stresses, forces and flows is clear and it is now widely appreciated that it will not be possible to master the transformations of living systems without adding physical understanding to the biological advances. The topic is particularly timely because of progress in the theories of active matter which describe the collective behaviour of systems out of thermodynamic equilibrium. We are using concepts such as activity-driven flows, motile topological defects, and active turbulence to study growth, motion and morphogenesis across a diversity of biological processes in mechanobiology and developmental biology.

Morphogenesis: (a) Protrusion growth at a +1 defect in a layer of confined, spindle-shaped, C2C12 myoblasts (Nature Materials,21:588, 2022). (b) Hydra tentacles (Nature Physics, 17:251, 2021). (c) Dynamics of an active shell from solving the active nematohydrodynamic equations of motion. The protrusion grows at a +1=2 active defect (Phys. Rev. Lett., 123:208001, 2019). (d) Invagination in the Drosophila embryo (Mechanisms of Development, 163:103629, 2020). (e) Continuum simulations showing the invagination of an active droplet. (f) Wrinkles induced by contractile activity: left: coloured by curvature, right: coloured by angle of the surface director (Phys. Rev. X, 11:021001, 2021).