Oxford Theoretical Physics
Condensed Matter Theory: Soft and Biological Matter
Julia Yeomans
Research:
Vacancies:
Group Members:
- Scott Edwards
- Nuno Silvestre
- Gareth Alexander
- Halim Kusumaatmaja
- Matthew Blow
- Richard Matthews
- Victor Putz
- Yiannis Zacharoudiou
- Anton Markesteijn
Collaborators:
- Anna Balazs
- Issam Ali
- Davide Marenduzzo
- Enzo Orlandini
- Olivier Pierre-Louis
Links:
- Oxford University
- Oxford Physics
- Theoretical Physics
- Condensed Matter Theory
- Theory of Soft and Biological Matter
Lecture Courses:
Back to current research interest
Low Reynolds number swimming
Microscopic organisms, such as bacteria and ciliated protozoa, swim in the low Reynolds number regime. This is analogous to humans trying to move in a very viscous liquid like treacle. Inertia is unimportant: once the swimmer ceases to move it stops instantly. The Stokes equations, which govern the zero Reynolds number limit, are invariant under time reversal and this means that to move at all the microswimmer must have a swimming stroke which is non-reciprocal in time.
We are using simple model swimmers to understand the hydrodynamics of swimming and the interactions that occur between organisms. One aim is to explore possible designs for fabricated microswimmers which could be used to carry payloads such as drugs. Another is to understand whether there are mechanisms whereby swimming bacteria can respond to the flow fields set up by their neighbours.
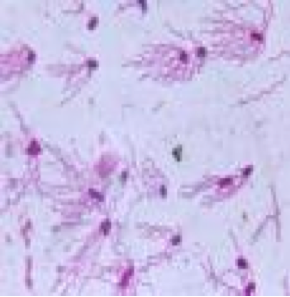 |
Left: E-coli bacteria swimming.
Right: a man-made microswimmer [1]. The head is a red blood cell; the tail a string of magnetic colloids. [1] Dreyfus et al., Nature 437, 862 (2005). |
 |
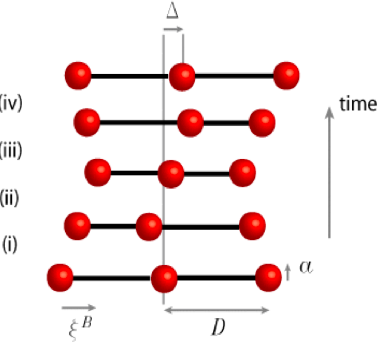 |
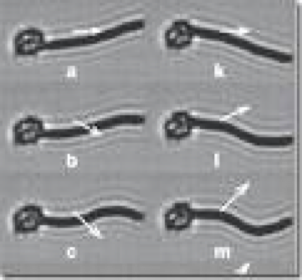
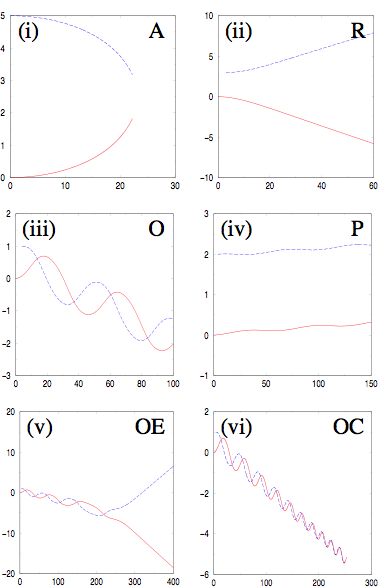
Left: Swimming stroke of a model low Reynolds number swimmer Right: Trajectories of two swimmers for different initial relative positions: the paths deviate from linear because of hydrodynamic interactions between the swimmers. |
 |
Recent Publications:
1. Dumb-bell swimmers, arxiv:0805.0733 [arxiv]
2. Hydrodynamic interactions between two swimmers at low Reynolds number, Phys. Rev. Lett. 99, 228103 (2007) [arxiv]
3. Modelling microscopic swimmers at low Reynolds number, J. Chem. Phys. 126, 064703 (2007) [arxiv]
